 |
|
 |
|
 |
In this paper, we have given an equational characterization of programs. Categorically, we have:
 |
|
 |
|
 |
 are given as a type-preserving relation between terms.
Following Milner's operational
semantics for action calculi, we would expect to have the categorical
picture:
are given as a type-preserving relation between terms.
Following Milner's operational
semantics for action calculi, we would expect to have the categorical
picture:
 'hello' 'hello' |
|
 'world' 'world' |
These 2-cells are generated from atomic reductions, in these examples:
 |
|||
 |
(where x + y = z) | ||
 |
 s s |
Unfortunately, we cannot just replay Milner's presentation in the premonoidal setting, since one of the axioms of a 2-category is functoriality of composition, which implies:
| If |    |
||
| and |    |
then |   ; ;  |
 'world' 'world' |
|
 'hello' 'hello' |
| If |    |
||
| and |  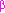  |
then |   ; ;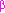  |
| If |    |
||
| and |  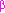  |
then |   ; ;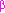  |
| If |    |
||
| and |    |
then |   ; ;  |
Formally, define
C  P
to be a pre-2-category whenever:
P
to be a pre-2-category whenever:
 Y]
(the central hom-category)
a category
P[X
Y]
(the central hom-category)
a category
P[X Y]
(the process hom-category).
Y]
(the process hom-category).
 Y]
is a subcategory of
P[X
Y]
is a subcategory of
P[X Y]
with the same objects (that is the same 1-cells).
Y]
with the same objects (that is the same 1-cells).
 Y]
Y]
 P[Y
P[Y Z]
Z]
 P[X
P[X Z]
Z]
 Y]
Y]
 P[Y
P[Y Z]
Z]
 P[X
P[X Z]
Z]
such that:
P[X Y] Y]
 P[Y
P[Y Z] Z]
|

|
P[X Z] Z]
|
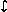
|
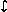
|
|
P[X Y] Y]
 P[Y
P[Y Z] Z]
|

|
P[X Z] Z]
|
and:
C[X Y] Y]
 P[Y
P[Y Z] Z]
|

|
C[X Y] Y]
 P[Y
P[Y Z] Z]
|
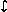
|
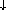
|
|
P[X Y] Y]
 P[Y
P[Y Z] Z]
|

|
P[X Z] Z]
|
commute.
Note that any 2-category is automatically a pre-2-category, since we can take C and P to be the same 2-category, and identify all of the hom-categories and composition functors.
We can then replay the definition of a premonoidal category at the 2-level to get a categorical presentation of a language with its operational semantics.
A premonoidal pre-2-category is a pre-2-category
C  P with:
P with:
 :
C
:
C  P
P  P
P
 :
P
:
P  C
C  P
P
such that:
 ,
,
 and
and
 coincide on objects,
coincide on objects,
 C to P
coincide, and
C to P
coincide, and
 Y
Y
 Y
Y  X
in P.
X
in P.
Following Power's presentation of
premonoidal categories as Subset-enriched categories, we can
present pre-2-categories using enriched categories. Define a category
to be centralized if some of its objects are tagged as central,
some of its morphisms are tagged as central, and satisfying the
property that if f : X  X
X and X is central, then
f and X
and X is central, then
f and X are central. Let Central be the
category of centralized categories with functors respecting the
central structure. Central has an asymmetric monoidal
structure where C * D is the subcategory of
C
are central. Let Central be the
category of centralized categories with functors respecting the
central structure. Central has an asymmetric monoidal
structure where C * D is the subcategory of
C  D where for any
pair of morphisms
(f,g) : (X,Y)
D where for any
pair of morphisms
(f,g) : (X,Y)  (X
(X ,Y
,Y ) either X
) either X is central or g is central. Then the above definition of a
pre-2-category is equivalent to a Central-category with
composition given as a functor P[X,Y] * P[Y,Z]
is central or g is central. Then the above definition of a
pre-2-category is equivalent to a Central-category with
composition given as a functor P[X,Y] * P[Y,Z]  P[X,Z]. We can then replay Power's
definition of a premonoidal category replacing
Subset-Cat with Central-Cat to find a
definition of a premonoidal pre-2-category equivalent to the above.
P[X,Z]. We can then replay Power's
definition of a premonoidal category replacing
Subset-Cat with Central-Cat to find a
definition of a premonoidal pre-2-category equivalent to the above.
For the closed structure, the isomorphisms:
 (Y
(Y  Z)]
Z)]
 V[(X
V[(X  Y)
Y)  Z]
Z]
 (Y
(Y  Z)]
Z)]
 C[(X
C[(X  Y)
Y)  Z]
Z]
 (Y
(Y  Z)]
Z)]
 P[(X
P[(X  Y)
Y)  Z]
Z]
allow value and central reductions to take place under function bodies, but not process reductions. For example we allow:

 'hello'
'hello'