 C
C
Given a symmetric monoidal category C: with a full subcategory (not necessarily symmetric monoidal) TC:
 C
C
a partial trace is a natural transformation:
 U A, Y
U A, Y  U A]
U A]
 C[X, Y]
C[X, Y]
satisfying certain axioms (given below, since they are much simpler to present graphically than equationally).
As an example, the categories
Cpo
 Cpo
(where the inclusion maps D
Cpo
(where the inclusion maps D to D)
have a partial trace given by fixed points.
to D)
have a partial trace given by fixed points.
As another example, given a signature with a subset of sorts defined to be traceable we can let C be the category of flow graphs over that signature where any cycle through the graph must pass through at least one edge labelled with a traceable sort, and TC be the full subcategory where the objects are traceable sorts. These categories have a partial trace given by forming a feedback loop:
We shall provide a different axiomatization of traces than that provided by Joyal, Street and Verity, but we shall show below that in the case when C and TC are the same category, we recover their definition. Note that these axioms are all graph isomorphisms, and indeed are a complete axiomatization for graph isomorphism.
Naturality in X
(for
f :
X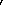
 X
and
g :
X
X
and
g :
X  U A
U A
 Y
Y  U A
in C):
U A
in C):
| = | ||
| f; TrX Y A (g) | = |
TrX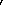 Y A
(f Y A
(f  idU A;
g)
idU A;
g)
|
Naturality in Y
(for
f :
Y
 Y
Y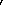 and
g :
X
and
g :
X  U A
U A
 Y
Y  U A
in C):
U A
in C):
| = | ||
| TrX Y A (g); f | = |
TrX Y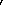 A
(g;
f A
(g;
f  idU A)
idU A)
|
Yanking:
| = | ||
| TrU(A) U(A) A (symmU(A) U(A)) | = | idU(A) |
Symmetry sliding
(for
f :
X  U(A)
U(A)  U(B)
U(B)
 Y
Y  U(B)
U(B)  U(A)):
U(A)):
| = | ||
TrX Y A
(Tr(X  U(A)) (Y U(A)) (Y  U(A)) B
(f;
(idY U(A)) B
(f;
(idY
 symmU(B) U(A)))
symmU(B) U(A)))
| = |
TrX Y B
(Tr(X  U(B)) (Y U(B)) (Y  U(B)) A
((idX U(B)) A
((idX
 symmU(B) U(A));
f)
symmU(B) U(A));
f)
|
Strength
(for
f :
V
 W
and
g :
X
W
and
g :
X  U A
U A
 Y
Y  U A
in C):
U A
in C):
| = | ||
f
 TrX Y A (g)
TrX Y A (g)
| = |
Tr(V  X) (W X) (W  Y) A
(f Y) A
(f
 g)
g)
|
For those readers familiar with Joyal, Street and Verity's axiomatization of a trace, the above axioms are obviously derivable from theirs. Moreover, the following lemmas show that we can derive their axiomatization, so in the case where TC and C coincide, our axiomatization is the same as theirs.
Lemma (Parameterized dinaturality)
(for
f :
Z  U(B)
U(B)
 U(A)
and
g :
X
U(A)
and
g :
X  U(A)
U(A)
 Y
Y  U(B)
in C):
U(B)
in C):
| = | ||
Tr(X  Z) Y A
((idX Z) Y A
((idX
 symmZ U(A));
(g
symmZ U(A));
(g
 idZ);
(idY
idZ);
(idY
 (symmU(B) Z);
f)))
(symmU(B) Z);
f)))
| = |
Tr(X  Z) Y B
((idX Z) Y B
((idX
 f);
g)
f);
g)
|

 U(A)
and
g :
X
U(A)
and
g :
X  U(A)
U(A)
 Y
Y  U(B)
in C):
U(B)
in C):
| = | ||
TrX Y A
(g;
(idY
 f))
f))
| = |
TrX Y B
((idX
 f);
g)
f);
g)
|
Proof.
Let Z be I in the above.

Lemma (Trace respects unit)
(for
f :
I
 U A
and
g :
X
U A
and
g :
X  U A
U A
 Y
in C):
Y
in C):
| = | ||
TrX Y A
(g;
idY
 f)
f)
| = |
(idX
 f);
g
f);
g
|

 U(C)
U(C)
 U(A)
and
g :
X
U(A)
and
g :
X  U(A)
U(A)
 Y
Y  U(B)
U(B)  U(C)
in C):
U(C)
in C):
| = | ||
TrX Y A
(g;
idY
 f)
f)
| = |
TrX Y C
(TrX Y B
((idX
 f);
g))
f);
g))
|

 W
and
g :
X
W
and
g :
X  U A
U A
 Y
Y  U A
in C):
U A
in C):
| = | ||
TrX Y A (g)
 f
f
| = |
Tr(X  V) (Y V) (Y  W) A
((idX W) A
((idX
 symmV U(A));
(g
symmV U(A));
(g
 f);
(idY
f);
(idY
 symmU(A) W))
symmU(A) W))
|