 M : T in C
M : T in C
| C | ::= | val |
| T | ::= | B |
| | | (T,...,T) | |
| | | C T : T |
| M | ::= | x |
| | | c M | |
| | | (M,...,M) | |
| | | fn C P {M} | |
| | | D M | |
| | | M M |
| D | ::= | let P = M; |
| | | D D | |
| | |
| P | ::= | x : T |
| | | (P,...,P) |
| C | ::= | x:T;...; x:T; |
C  M : T in C
M : T in C
| [x not in C'] | ||||||
|
[c : B1,...,Bm  C1,...,Cn in C] C1,...,Cn in C]
| |||||||||
| C |  |
M1 : T1 in C |
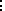 |
||
| C |  |
Mn : Tn in C |
| C |  |
(M1,...,Mn) : (T1,...,Tn) in C |
| C |  |
(P : T) : C' |
| C C' |  |
M : T' in C |
| C |  |
fn C P {M} : (C T : T') in val |
| C |  |
D : C' in C |
| C C' |  |
M : T in C |
| C |  |
D M : T in C |
| C |  |
M : (C T : T') in val |
| C |  |
M' : T in C |
| C |  |
M M' : T' in C |
C  D : C in C
D : C in C
| C |  |
(P : T) : C' |
| C |  |
M : T in C |
| C |  |
let P = M : C' in C |
| C |  |
D1 : C1 in C |
| C C1 |  |
D2 : C2 in C |
| C |  |
D1 D2 : C1 C2 in C |
| C |  |
() : () in C |
C  (P : T) : C
(P : T) : C
| C |  |
((x : T) : T) : (x : T) |
| [Ci have disjoint vars] | |||||||||||||||
Equations for terms are alpha-conversion plus:
| let P = M; P | = | M | |
| let P = P; M | = | M | |
| (D D') M | = | D (D' M) | |
| D let P = M; M' | = | let P = (D M); M' | (bv D  fv M' = Ø) fv M' = Ø) |
| D (fn C P {M}) | = | fn C P {D M} | (bv D  bv P = Ø) bv P = Ø) |
| D (M M') | = | (D M) M' | (bv D  fv M' = Ø) fv M' = Ø) |
| D (M M') | = | M (D M') | (bv D  fv M = Ø) fv M = Ø) |
| (fn C P {M}) M' | = | let P = M'; M | |
| fn C P {M P} | = | M | |
| D (M1,...,Mn) | = | (D M1,...,D Mn) |
Equations for declarations are alpha-conversion plus:
| let P = (D P) | = | D | (bv P = bv D) |
| let (P1,...,Pn) = (M1,...,Mn); | = | let P1 = M1;...; let Pn = Mn; | (bv Pi  fv Mj = Ø) fv Mj = Ø) |
| (D; D'); D'' | = | D (D' D'') | |
| D () | = | D | |
| () D | = | D | |
| D D' | = | D' D |
(bv D  fv D' =
fv D fv D' =
fv D  bv D' =
Ø) bv D' =
Ø)
|
We shall write `C  M =
M' : T in val' and `C
M =
M' : T in val' and `C
 D = D' : T in val' for the typed proof system given by the above
axioms.
D = D' : T in val' for the typed proof system given by the above
axioms.
Let val be the category with:
 M : (U)
in val
M : (U)
in val
viewed up to alpha-conversion and provable equality.
 (x) : (T)
in val
(x) : (T)
in val
 M : (U)
in val) ;
(y : U
M : (U)
in val) ;
(y : U
 N : (V)
in val)
N : (V)
in val)
is given by let-binding:
 let (y : U) = M;
N : (V)
in val)
let (y : U) = M;
N : (V)
in val)
where x is the vector x1...xn, and T is the vector T1...Tn.
The category val is cartesian closed, with (using alpha-conversion to avoid variable name clashes):
 M : (T')
in val)
M : (T')
in val)
 (y : U
(y : U
 N : (U')
in val)
N : (U')
in val)
is given by pairing:
 let (x' : T') = M;
let (y' : U') = N;
(x'y') : (T'U')
in val
let (x' : T') = M;
let (y' : U') = N;
(x'y') : (T'U')
in val
 (xx) : (TT)
in val
(xx) : (TT)
in val
 (yx) : (UT)
in val
(yx) : (UT)
in val
 () : ()
in val
() : ()
in val
 V
is given by function type
val (U):(V).
V
is given by function type
val (U):(V).
 M : (V)
in val
M : (V)
in val
is given by an anonymous function:
 fn val (y : U)
{M} : (val (U):(V))
in val
fn val (y : U)
{M} : (val (U):(V))
in val
 M : (val (U):(V))
in val
M : (val (U):(V))
in val
is given by function application:
 M (y) : (V)
in val
M (y) : (V)
in val
We shall now give a graphical presentation of a cartesian closed category, which allows us to draw data-flow diagrams for programs in val.
The symmetric monoidal structure is drawn:
| Identity: | Composition: |
| Tensor: | |
| Symmetry: | |
The product structure is drawn:
| Diagonal: | |
| Terminal: | |
The closed structure is drawn:
| Currying: | |
| Evaluation: |
| Left unit: | = | ||
| Right unit: | = | ||
| Associativity: | = | ||
| Functoriality of tensor wrt identity: | = | ||
| Functoriality of tensor wrt composition: | = | ||
| Symmetry is an iso: | = | ||
| Symmetry is natural: | = |
As well as the symmetric monoidal category axioms, we have diagonal and terminal natural transformations, so the category has finite products. Note that these axioms are not graph isomorphisms.
| Diagonal is natural: | = | ||
| Terminal is natural: | = |
Finally, we have the axioms for a cartesian closed category. Again, these are not graph isomorphisms.
| Beta-conversion: | = | ||
| Eta-conversion: | = | ||
| Naturality of currying: | = |
Note that we have only given one naturality axiom: that in the adjunction:
 Z]
Z]
 V[X
V[X  Y, Z]
Y, Z]
currying is natural in X. The other three naturality axioms are derivable, for example the naturality of uncurrying in Z is given by the beta-conversion: