 V
is:
V
is:
The flow graphs we consider in this paper are finite directed edge-labelled, node-labelled graphs where the incoming and outgoing edges to each node are ordered, and each edge has exactly one start node, but multiple finish nodes. We impose a type discipline to ensure that the edge and node labels match. These graphs are the same as Hasegawa's sharing graphs.
A single-coloured flow graph G over a signature
 V
is:
V
is:
 F.
F.
 F.
F.
 F,
N : c and
c : X
F,
N : c and
c : X  Y,
then
E : X and F : Y.
Y,
then
E : X and F : Y.
| Identity: | Composition: |
| Tensor: | |
| Symmetry: | |
| Diagonal: | |
| Terminal: | |
A morphism F between flow graphs G and G is:
is:
 .
.
 .
.
| Naturality of diagonal: | 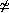 |
||
| Terminal is natural: | 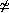 |
A relation R between flow graphs G and G is:
is:
 .
.
 .
.
 and E : X then E
and E : X then E : X,
: X,
 and N : c then N
and N : c then N : c,
: c,
 F
and G
F
and G : E
: E
 F
F then E R E
then E R E and F R F
and F R F , and
, and
 F in G,
N
F in G,
N : E
: E
 F
F in G
in G and N R N
and N R N then E R E
then E R E and F R F
and F R F .
.
 R
R  G
G in the category of flow graphs.
in the category of flow graphs.
A relation R between flow graphs G and G is a
simulation iff:
is a
simulation iff:
 then
E
then
E is the nth outgoing edge of N
is the nth outgoing edge of N in G
in G and N R N
and N R N .
.
 of G
of G such that
E R E
such that
E R E ).
).
 is a
bisimulation iff R and R-1 are simulations.
is a
bisimulation iff R and R-1 are simulations.
G and G are bisimilar (written
G
are bisimilar (written
G  G
G )
iff there is a bisimulation between them.
)
iff there is a bisimulation between them.
Note that any graph isomorphism is a simulation, and so isomorphic graphs are bisimilar. The converse is not true, since:
 |
||
 |
 of G
of G such that
E R E
such that
E R E ).
).
Proposition (Bisimulation is a congruence). Bisimulation is a congruence wrt the graph operations.

 iff:
iff:
 Y1...Yn
Y1...Yn


 [[Xm]]
[[Xm]]  [[Y1]]
[[Y1]] 

 [[Yn]].
[[Yn]].
 V form a category
Graph(
V form a category
Graph( V) over
V) over  V where:
V where:
 F
such that E : X and
F : Y, viewed up to bisimulation.
F
such that E : X and
F : Y, viewed up to bisimulation.
Proposition (Flow graphs form a category with finite products).
Graph( V) is a strict cartesian category over
V) is a strict cartesian category over  V.
V.
Proof.
We have already defined the required operations, but we need to
show they satisfy the axioms for a cartesian category.
For this, we construct a bisimulation for each of the axioms.

Since flow graphs over  V
form a cartesian category over
V
form a cartesian category over  V, there is a unique
morphism [[_]] from the free cartesian category over
V, there is a unique
morphism [[_]] from the free cartesian category over
 V into Graph(
V into Graph( V). We can
define this syntactically as the term algebra (with the type system
and axiomatization given for cartesian categories)
Term(
V). We can
define this syntactically as the term algebra (with the type system
and axiomatization given for cartesian categories)
Term( V):
V):
| f,g | ::= | idX | |
| | | f ; g | ||
| | | f  g g |
||
| | | symmX Y | ||
| | | copyX | ||
| | | discardX | ||
| | | c |
If terms can be proved equal using the axioms for a cartesian category
we shall write
 f = g.
f = g.
We would like to show soundness and completeness for this axiomatization,
that is
 f = g
iff
[[f]]
f = g
iff
[[f]]  [[g]].
As is usual for such results, soundness is immediate, but completeness
requires a normal form result. Most of the rest of this section is
taken up by showing the required normalization results.
[[g]].
As is usual for such results, soundness is immediate, but completeness
requires a normal form result. Most of the rest of this section is
taken up by showing the required normalization results.
Proposition (Soundness).
If  f = g
then [[f]]
f = g
then [[f]]  [[g]].
[[g]].
Proof.
Follows immediately from the fact that Graph( V)
is a cartesian category.
V)
is a cartesian category.

Proposition (Expressivity).
For any graph G, there is a term f
such that [[f]]  G.
G.
Proof.
Proved by induction on the number of outgoing edges of G.

A shuffle (ranged over by s) is any term not including constructors c. A permutation (ranged over by p) is any shuffle not including copy or discard.
Proposition (Completeness for shuffles).
If [[s1]]  [[s2]]
then
[[s2]]
then  s1 = s2.
s1 = s2.

| n | ::= | |
| | | ||
| | |
 f = g.
f = g.
Proof.
First show by induction on syntax that for any normal f1 and f2, we can find
normal g such that
 f1
f1  f2 = g.
f2 = g.
Then show by induction on syntax that for any normal f and shuffle s, we can find
normal g such that
 f;s = g.
f;s = g.
Then show by induction on syntax that for any normal f1 and f2, we can find
normal g such that
 f1;f2 = g.
f1;f2 = g.
Finally show by induction on syntax that for any f, we can find normal g such
that  f = g.
f = g.

Define p_inv to be the permutation:
 q)_inv =
p_inv
q)_inv =
p_inv  q_inv
q_inv
Proposition (Permutations are isos).
For any p,
 p;p_inv = id
and
p;p_inv = id
and
 p_inv;p = id.
p_inv;p = id.
Proof. An induction on p.

Proposition (Cancellation of permutations). For any:

 =
=

Proof. Let h be: f;p_inv. Then use soundness and p being an iso to show the required properties.

Proposition (Cancellation of nodes). For any:

 =
=


 [[g]]
then
[[g]]
then  f = g.
f = g.
Proof.
Find the normal form equal to g, and then
cancel permutations and nodes iteratively,
finishing with a use of completeness for shuffles,
to prove  f = g.
f = g.

Proposition (Initiality).
Graph( V) is the initial
cartesian category over
V) is the initial
cartesian category over  V.
V.
Proof.
By construction, Term( V) is the initial cartesian
category over
V) is the initial cartesian
category over  V.
Since Term(
V.
Since Term( V) is expressive, we
have a map term : Graph(
V) is expressive, we
have a map term : Graph( V)
V)  Term(
Term( V) with the property that
[[term(G)]]
V) with the property that
[[term(G)]]  G. By
soundness and completeness, this map is an isomorphism
in the category of categories with finite products
over
G. By
soundness and completeness, this map is an isomorphism
in the category of categories with finite products
over  V, and so
Graph(
V, and so
Graph( V) is the initial cartesian category
over
V) is the initial cartesian category
over  V.
V.
