Value category

Syntax

A signature is:

A set of sorts (ranged over by X, Y, Z).
A set of constructors (ranged over by c, d).
For each constructor, a source and target vector of sorts, written c : X Y.

Given a signature

_V, define the language Exp(

_V) as having types:

T	::=	X	(Base type, X in _V)
	\|	(T,...,T)	(Tuple type)

expressions:

M	::=	x	(Variable)
	\|	c M	(Value constructor, c in _V)
	\|	(M,...,M)	(Tuple expression)
	\|	D M	(Declaration binding)

declarations:

D	::=	let P = M;	(Singleton declaration)
	\|	D D	(Composition of declarations)
	\|		(Singleton declaration)

and patterns:

P	::=	x : T	(Singleton pattern)
	\|	(P,...,P)	(Tuple pattern)

This language is similar to de Paiva and Ritter's lambda-calculus with explicit substitutions, although we have presented explicit substitutions as declarations.

In examples, we will use some syntax sugar, for example writing 1 + 2 for +(1(),2()).

The novel feature of the type system for this language is to tag the judgements with a category C to determine whether the expression is a value expression, a central expression, or a process expression:

M : T in C

For example the expression 1 + 2 is entirely composed of value constructors, so is in the val category:

(1 + 2) : int in val

whereas set(1 + 2) contains a process constructor, so is in the process category:

set(1 + 2) : () in proc

For this section, we shall only consider value constructors, so the only category we need consider is val. Later sections will introduce the central and proc categories.

::=

val

With this exception, the type system is given as usual for the term algebra with declarations, using contexts:

::=

x : T,..., x : T

The judgements for expressions are of the form M : T in C, and are given for variables:


, x:T,		x : T in C

[x not in

]

value constructors:

		M : (B₁,...,B_m) in val

		c M : (C₁,...,C_n) in val

[c : B₁,...,B_m

C₁,...,C_n in

_V]

tuples:

		M₁ : T₁ in C

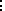		M_n : T_n in C

		(M₁,...,M_n) : (T₁,...,T_n) in C

and declaration bindings:

		D : in C
,		M : T in C

		D M : T in C

Judgements for declarations are of the form D : in C and are given for singleton declarations:

		(P : T) :
		M : T in C

		let P = M; : in C

composition of declarations:

		D₁ : ₁ in C
, ₁		D₂ : ₂ in C

		D₁ D₂ : ₁, ₂ in C

[

₁ and

₂ disjoint]

and empty declarations:


		() : () in C

Judgements for patterns are of the form (P : T) : and are given for singleton patterns:


		((x : T) : T) : (x : T)

and tuple patterns:

		(P₁ : T₁) : ₁

		(P_n : T_n) : _n

		((P₁,...,P_n) : (T₁,...,T_n)) : (₁,...,_n)

[

_i have disjoint vars]

Graphical semantics

The semantics of a type is given as a vector of sorts:

[[X]] = X [[(T₁,...,T_n)]] = [[T₁]],...,[[T_n]]

The semantics of a context is given as a vector of sorts:

[[x₁:T₁,...,x_n:T_n]] = [[T₁]],...,[[T_n]]

The semantics of terms is given as a flow graph (defined formally in an appendix):

[[

M : T in val]] : [[

]]

[[T]]

These graphs can be drawn with incoming edges on the left and outgoing edges on the right:

We shall usually elide the context and types where they are obvious. The semantics is defined inductively:

[[x in val]]	=
[[c M in val]]	=
[[(M1,...,Mn) in val]]	=
[[D M in val]]	=

The semantics of declarations is given as a graph:

[[

D :

in val]] : [[

]]

[[

]]

The semantics is defined inductively:

[[let P = M; in val]]	=
[[D1 D2 in val]]	=
[[ in val]]	=

For example, here are four graphs for the same arithmetic expression:


return ((1+1)*(1+1));	let x:int = 1+1;	let y:int = 1;	let y:int = 1;
	return (x*x);	return ((y+y)*(y+y));	let x:int = y+y;
			return (x*x);

These graphs can be proved equal using the axioms for a category with finite products, but they are not graph isomorphic. This means that graph isomorphism is not an appropriate equivalence on graphs if we wish to build the initial category with finite products over _V. Instead, in an appendix we define an appropriate notion of bisimulation on flow graphs, and construct a category Graph(_V) where:

Objects are vectors of sorts.
Morphisms are acyclic flow graphs, viewed up to bisimulation.

We show that Graph(

_V) is the initial strict cartesian category over

_V. Thus the graphical semantics defined above uniquely determines a semantics in any category with finite products over

_V.

Previous | Next